-
This is the tutorial for explaining how to read the charts.
This is for the 7 string augmented chord guitar tuning, Ralph Patt style, also known as M3.
This gets off to a slow start but then, if you are in a particular audience, it gets off rolling and will become completely fascinating,
such that you can stare at it for years.
Tutorial, section 1
The numbers 0-11, with the number 0 representing the root note,
and after reaching 11 the count resumes again with 0 in the next octave.
0,1,2,3,4,5,6,7,8,9,10,11,0
The numbers 0-11 with the number 10 represented as j and the number 11 represented as k,
so as to allow 10 and 11 to be represented by single digits.
0123456789jk0
The numbers 0-11 shown as on the Ralph Patt Augmented tuning.
| * . . . | . * . . | . . * . | . . . * . | 0 1 2 3 | k 0 1 2 | j k 0 1 | 9 j k 0 . | 8 9 j k | 7 8 9 j | 6 7 8 9 | 5 6 7 8 . | 4 5 6 7 | 3 4 5 6 | 2 3 4 5 | 1 2 3 4 . | 0 1 2 3 | k 0 1 2 | j k 0 1 | 9 j k 0 . | * . . . | . * . . | . . * . | . . . * .
The 7 most practical diads, two string chords.
1 semitone:2 semitones:| * . . . | . * . . | . . * . | . . . * . | x . . . . | . . . x . | . . . . . | 1 . . . . | . . . 0 . | * . . . | . * . . | . . * . | . . . * . 3 semitones:| * . . . | . * . . | . . * . | . . . * . | x . . . . | . . x . . | . . . . . | 2 . . . . | . . 0 1 . | * . . . | . * . . | . . * . | . . . * . 4 semitones:| * . . . | . * . . | . . * . | . . . * . | x . . . . | . x . . . | . . . . . | 3 . . . . | . 0 1 2 . | * . . . | . * . . | . . * . | . . . * . 5 semitones:| * . . . | . * . . | . . * . | . . . * . | x . . . . | x . . . . | . . . . . | 4 . . . . | 0 1 2 3 . | * . . . | . * . . | . . * . | . . . * . 6 semitones:| * . . . | . * . . | . . * . | . . . * . | . x . . . | x . . . . | . . . . . | 4 5 . . . | 0 1 2 3 . | * . . . | . * . . | . . * . | . . . * . 7 semitones:| * . . . | . * . . | . . * . | . . . * . | . . x . . | x . . . . | . . . . . | 4 5 6 . . | 0 1 2 3 . | * . . . | . * . . | . . * . | . . . * . | * . . . | . * . . | . . * . | . . . * . | . . . x . | x . . . . | . . . . . | 4 5 6 7 . | 0 1 2 3 . | * . . . | . * . . | . . * . | . . . * .
-
02-10-2020 04:39 PM
-
Actually I was just getting to the part about the octaves, pluck them with your pinky and middle finger, I find it is very pleasant. The unison diad, 0:
The unison diad plus the 5th, 50:| * . . . | . * . . | . . * . | . . . * . | x . . . . . | . . . . x . | . . . . . . | 0 . . . . . | . . . . 0 . | * . . . | . * . . | . . * . | . . . * . The unison diad plus the flat 6th, 04:| * . . . | . * . . | . . * . | . . . * . | x . . . . . | . . . . x . | . . . x . . | * . . . | . * . . | . . * . | . . . * . The common, 5th power chord, 75:| * . . . | . * . . | . . * . | . . . * . | x . . . . . | x . . . . . | . . . . x . | * . . . | . * . . | . . * . | . . . * . The 4th power chord, 57:| * . . . | . * . . | . . * . | . . . * . | . . . . x . | . . . x . . | x . . . . . | * . . . | . * . . | . . * . | . . . * . One octave, two notes which are 12 semitones apart, may be plucked using two fingers,middle and pinky, while still holding a pick:| * . . . | . * . . | . . * . | . . . * . | . . . . x . | . x . . . . | x . . . . . | * . . . | . * . . | . . * . | . . . * . A triad contains 3 notes, the root of the triad plus 2 other notes, the other 2 notes are adding color to the highest note, therefore the highest note is the root of the triad. The root of the triad is not the same as the root of the scale in which the triad occurs. The triad is named based on the number of semitones between each of the notes, from lowest to highest. To describe 3 notes by the distances between the 3 notes, 2 numbers are required, the distance from the lowest note to the middle note, then the distance from the middle note to the highest note. But in order to understand the inversions of the triad, a fourth note is added, that is the root, that is the note exactly 12 semitones lower than the high note. Example: 35 aka 435Therefore the triad named as 35 for example, may also be named 435. The 4 is a foregone conclusion since the 3 numbers must add up to 12, since the two roots in the chord are 12 semitones apart. In order to understand the inversions of the triad, 3 digits are used and they must add up to 12, so we can understand that 435/354/543 are the inversions. However 35 itself is what you are playing, with 3 notes, representing the highest note with a flourish of full color added, and lightweight and quick. 35 implies 2 intervals, which implies a 3 string chord. 435 implies 3 intervals and 4 notes. The difference between 35 and 435 is that 435 includes the top note in two octaves. See this example of why this shape is named 35 and why it may also be named 435. The lowest note is the same note as the highest note, exactly 12 semitones lower.| * . . . | . * . . | . . * . | . . . * . | . . x . . | . . . . . | . . . . . | . . x . . | . . . . . | j k 0 . . | 6 7 8 9 . | 2 3 4 5 . | . . 0 1 . | * . . . | . * . . | . . * . | . . . * . | * . . . | . * . . | . . * . | . . . * . | . x . . . | x . . . . | . x . . . | . x . . . | . . . . . | k 0 . . . | 7 8 9 j . | 3 4 5 6 . | . 0 1 2 . | . . . . . | . 5 . . . | 3 . . . . | . 4 . . . | . 0 . . . | . . . . . | 4 5 . . . | 3 1 2 3 . | 3 4 1 2 . | . 0 1 2 . | . . . . . | . x . . . | x . . . . | . x . . . | . . . . . | . 5 . . . | 3 . . . . | . 0 . . . | . . . . . | 4 5 . . . | 3 1 2 3 . | . 0 1 2 . | * . . . | . * . . | . . * . | . . . * .
-
The most practical triads, 3 string chords. 435/354/543 - inversions of 435, the major triad35 aka 435
54 aka 354| * . . . | . * . . | . . * . | . . . * . | . x . . . | x . . . . | . x . . . | * . . . | . * . . | . . * . | . . . * . 43 aka 543| * . . . | . * . . | . . * . | . . . * . | . x . . . | . x . . . | x . . . . | * . . . | . * . . | . . * . | . . . * . 453/534/345 - inversions of 453, the minor triad53 aka 453| * . . . | . * . . | . . * . | . . . * . | x . . . . | . x . . . | . x . . . | * . . . | . * . . | . . * . | . . . * . 34 aka 534| * . . . | . * . . | . . * . | . . . * . | x . . . . | . x . . . | x . . . . | * . . . | . * . . | . . * . | . . . * . 45 aka 345| * . . . | . * . . | . . * . | . . . * . | x . . . . | x . . . . | . x . . . | * . . . | . * . . | . . * . | . . . * . 525/255/552 - inversions of 525, the suspended triad25 aka 525| * . . . | . * . . | . . * . | . . . * . | . x . . . | x . . . . | x . . . . | * . . . | . * . . | . . * . | . . . * . 55 aka 255| * . . . | . * . . | . . * . | . . . * . | . x . . . | x . . . . | . . x . . | * . . . | . * . . | . . * . | . . . * . 52 aka 552| * . . . | . * . . | . . * . | . . . * . | . . x . . | . x . . . | x . . . . | * . . . | . * . . | . . * . | . . . * . 363/633/336 - inversions of 363, the diminished triad63 aka 363| * . . . | . * . . | . . * . | . . . * . | x . . . . | . . x . . | . x . . . | * . . . | . * . . | . . * . | . . . * . 33 aka 633| * . . . | . * . . | . . * . | . . . * . | . x . . . | . . x . . | x . . . . | * . . . | . * . . | . . * . | . . . * . 36 aka 336| * . . . | . * . . | . . * . | . . . * . | x . . . . | . x . . . | . . x . . | * . . . | . * . . | . . * . | . . . * . 444 - which has no inversions, the augmented triad44 aka 444| * . . . | . * . . | . . * . | . . . * . | . . x . . | x . . . . | . x . . . | * . . . | . * . . | . . * . | . . . * . | * . . . | . * . . | . . * . | . . . * . | . . x . . | . . x . . | . . x . . | * . . . | . * . . | . . * . | . . . * .
-
372/723/237 - inversions of 372, the minor 7 minus 5 triad72 aka 372
23 aka 723| * . . . | . * . . | . . * . | . . . * . | . x . . . | . . . x . | x . . . . | * . . . | . * . . | . . * . | . . . * . 37 aka 237| * . . . | . * . . | . . * . | . . . * . | x . . . . | . x . . . | . . . x . | * . . . | . * . . | . . * . | . . . * . 732/327/273 - inversions of 732, the minor 7 minus 3 triad32 aka 732| * . . . | . * . . | . . * . | . . . * . | . . . x . | x . . . . | . x . . . | * . . . | . * . . | . . * . | . . . * . 27 aka 327| * . . . | . * . . | . . * . | . . . * . | x . . . . | . . x . . | . . . x . | * . . . | . * . . | . . * . | . . . * . 73 aka 273| * . . . | . * . . | . . * . | . . . * . | . . . x . | x . . . . | . . x . . | * . . . | . * . . | . . * . | . . . * . 741/417/174 - inversions of 741, the major 7 minus 3 triad41 aka 741| * . . . | . * . . | . . * . | . . . * . | . . x . . | . . . x . | x . . . . | * . . . | . * . . | . . * . | . . . * . 17 aka 417| * . . . | . * . . | . . * . | . . . * . | x . . . . | . . . x . | . . . x . | * . . . | . * . . | . . * . | . . . * . 74 aka 174| * . . . | . * . . | . . * . | . . . * . | . . . x . | x . . . . | . . . x . | * . . . | . * . . | . . * . | . . . * . 471/714/147 - inversions of 471, the major 7 minus 5 triad71 aka 471| * . . . | . * . . | . . * . | . . . * . | . . . x . | . . . x . | x . . . . | * . . . | . * . . | . . * . | . . . * . 14 aka 714| * . . . | . * . . | . . * . | . . . * . | x . . . . | . . . x . | x . . . . | * . . . | . * . . | . . * . | . . . * . 47 aka 147| * . . . | . * . . | . . * . | . . . * . | x . . . . | x . . . . | . . . x . | * . . . | . * . . | . . * . | . . . * . | * . . . | . * . . | . . * . | . . . * . | . . . x . | x . . . . | x . . . . | * . . . | . * . . | . . * . | . . . * .
-
165/651/516 - inversions of 165, the flat 9 minus 3 triad65 aka 165
51 aka 651| * . . . | . * . . | . . * . | . . . * . | . . . x . | . . x . . | x . . . . | * . . . | . * . . | . . * . | . . . * . 16 aka 516| * . . . | . * . . | . . * . | . . . * . | x . . . . | . . . x . | . . x . . | * . . . | . * . . | . . * . | . . . * . 156/561/615 - inversions of 156, the flat 9 flat 5 minus 3 triad56 aka 156| * . . . | . * . . | . . * . | . . . * . | . . x . . | x . . . . | . . . x . | * . . . | . * . . | . . * . | . . . * . 61 aka 561| * . . . | . * . . | . . * . | . . . * . | . . . x . | . x . . . | x . . . . | * . . . | . * . . | . . * . | . . . * . 15 aka 615| * . . . | . * . . | . . * . | . . . * . | x . . . . | . . . x . | . x . . . | * . . . | . * . . | . . * . | . . . * . 462/624/246 - inversions of 462, the dominant minus 5 triad62 aka 462| * . . . | . * . . | . . * . | . . . * . | . x . . . | x . . . . | . . . x . | * . . . | . * . . | . . * . | . . . * . 24 aka 624| * . . . | . * . . | . . * . | . . . * . | x . . . . | . . x . . | x . . . . | * . . . | . * . . | . . * . | . . . * . 46 aka 246| * . . . | . * . . | . . * . | . . . * . | x . . . . | x . . . . | . . x . . | * . . . | . * . . | . . * . | . . . * . 426/264/642 - inversions of 426, the major flat 5 triad26 aka 426| * . . . | . * . . | . . * . | . . . * . | . . x . . | x . . . . | x . . . . | * . . . | . * . . | . . * . | . . . * . 64 aka 264| * . . . | . * . . | . . * . | . . . * . | . . x . . | x . . . . | . . x . . | * . . . | . * . . | . . * . | . . . * . 42 aka 642| * . . . | . * . . | . . * . | . . . * . | . . x . . | . . x . . | x . . . . | * . . . | . * . . | . . * . | . . . * . | * . . . | . * . . | . . * . | . . . * . | x . . . . | . . x . . | . . x . . | * . . . | . * . . | . . * . | . . . * .
-
Depending on the scale in which you are playing, each note of the scale will have different diads and triads available for the coloring of that note. The scale and the diads and triads within it may be mapped in a diagram. To understand the unique triads available, just one inversion of each triad may be mapped in a separate diagram. Most of the scales I have mapped contain a sequence from the circle of fifths. If the scale contains a sequence from the circle of fifths I have mapped those scale positions according to the classical mode letting, BEADGCF for 7 notes, EADGC for 5 notes. Hexatonic Marwa, Hexatonic Purabi (hexatonic purabi is not a raga), and Hexatonic Todi each contain 5 notes in sequence from the circle of fifths, plus the root note which is out of sequence, these 6 noted scales I have noted as r for root, plus EADGC. Bhairab/Byzantine does not contain more than 3 sequential notes from the circle of fifths, so I have noted those 7 scale positions as SRGMPDN according to the Indian notation which uses the first letter of the Sanskrit names for the numbers with S=1,R=2,G=3,M=4,P=5,D=6,N=7, which are pronounced as Sa Re Ga Ma Pa Da Ni, and which have the same meaning as the solfeggio system which is Do Re Mi Fa So La Ti.
The Western and Hindustani classical Indian names of the classical mode scales are E=phrygian=bhairabi, A=aeolian=asabari, D=dorian=kafi, G=mixolydian=khamaj, C=ionian=bilabal, F=lydian=kalyan, and B which is locrian is not recognized in Hindustani music. Marwa hexatonic is an inversion of the minor blues hexatonic. In order to understand that the classical modes are inversions of each other, they may be written as an interval sequence, A=2122122,B=1221222,C=2212221,D=2122212,E=1222122, F=2221221,G=2212212. In order to understand that the blues pentatonics are inversions of each other, they may be written as D=suspended=23232, E=mangong=32322, G=ritusen=23223, A=minor=32232, C=major=22323. These are named according to the length of the spaces between each note, for example the suspended pentatonic is 23232, 4 notes plus the root, R.X..X.X..X.R. BEADGCF and EADGCF represent the order of the notes in the circle of fifths. The 7 classical modes are all sequences of 7 notes from the circle of fifths. The 5 blues pentatonics are all sequences of 5 notes from the circle of fifths. From B to E is 5 semitones, from E to A is 5 semitones, from A to D is 5 semitones, from D to G is 5 semitones, from G to C is 5 semitones, from C to F is 5 semitones. From F to C is 7 semitones, from C to G is 7 semitones, from G to D is 7 semitones, from D to A is 7 semitones, from A to E is 7 semitones, from E to B is 7 semitones. Where you have 3 notes in sequence from the circle of fifths, there you will have the suspended triad and its 2 inversions.. The classical modes and blues pentatonics can be played in any tonal root, in other words, the root of ionian does not have to be tonal C, the root of dorian does not have to be tonal D, etc. The letters BEADGCF are used to show the order in which the inversions and intervals occur.. Therefore, this is the meaning of the charts, which show the full triad mapping of each scale.. Summary of the triad groups. If you have skipped to the end of the document, the reason for these groups and the notation used, is so you can understand the inversions.. I am fighting very hard to get line breaks in this text editor.. The triad groups are:. -Suspended: 525/255/552. -. Major: 435/354/543. Minor: 453/534/345. -. Diminished: 363/633/336. -. Minor 7 minus 5th: 372/723/237. Minor 7 minus 3rd: 732/327/273. -. Major 7 minus 5th: 471/714/147. Major 7 minus 3rd: 741/417/174. -. Flat 9 minus 3rd: 165/651/516. Flat 9 flat 5 minus 3rd: 156/561/615. -. Major flat 7: 426/264/642. Dominant minus 5th: 462/624/246. -. This is the end of the explanation about how to read the charts.. Last edited by KooksAmass; 02-11-2020 at 03:52 PM.
-
* Classical modes - D-EF-G-A-BC-D - BEADGCF - B-locrian, E=phrygian, A=aeolian, D=dorian=2122212, G=mixolydian, C-ionian, F=lydian * 3-5-7 D 43 - 45 *All* *All* D 63 D -45-7 E 34 - 45 - 54 25 - 52 27 - 32 - 72 E 14 - 47 - 74 65 E 3-56- F 35 - 53 55 23 - 73 F 33 41 - 71 15 - 51 26 - 46 F 3-5-7 G 35 - 43 - 53 *All* 23 - 32 - 37 - 73 G 17 62 G -45-7 A 34 - 45 - 54 *All* 27 - 32 - 37 - 72 A 14 64 A -4-67 B 34 - 54 52 27 - 72 B 36 47 - 74 16 - 56 24 - 42 B 3-5-7 C 35 - 43 - 53 25 - 55 23 - 37 - 73 C 17 - 41 - 71 61 C Unique: 35@G - 35@C - 35@F - 53@G - 53@C - 53@F 63@D 23@D - 23@G - 23@C - 23@F - 32@E - 32@A - 32@D - 32@G 25@E - 25@A - 25@D - 25@G - 25@C 47@B - 47@E - 74@B - 74@E 65@E - 56@B 46@F - 64@A | * . . . | . * . . | . . * . | . . . * . | D . E F | . D . E | C . D . | B C . D . | . B C . | A . B C | . A . B | G . A . . | . G . A | F . G . | E F . G | . E F . . | D . E F | . D . E | C . D . | B C . D . | . B C . | A . B C | . A . B | G . A . . | . G . A | F . G . | E F . G | . E F . . | * . . . | . * . . | . . * . | . . . * .
-
* Marwa - 132321 - Re--g-a--c-dR - EADGC - pentatonics E=mangong;A=minor;D=suspended;G=ritusen;C=major * 3--6- r 53 r 33 71 51 - 56 26 r -4--7 E 54 - 34 52 72 - 27 E 61 E 345-7 G 43 - 34 55 - 25 23 - 37 - 73 G 14 64 G --567 A 45 25 - 52 72 - 32 - 27 A 36 15 - 16 42 A 3-5-- C 35 - 53 - 45 55 23 - 73 C 63 C --5-7 D 55 - 25 - 52 37 - 32 D 47 65 D Unique: 53@r - 53@C - 35@C 25@G - 25@A - 25@D 23@G - 23@C - 32@A - 32@D 63@C 47@D 65@D - 56@r 64@G | * . . . | . * . . | . . * . | . . . * . | r E . . | D r E . | . D r E | C . D r . | . C . D | . . C . | A . . C | . A . . . | G . A . | . G . A | . . G . | E . . G . | r E . . | D r E . | . D r E | C . D r . | . C . D | . . C . | A . . C | . A . . . | G . A . | . G . A | . . G . | E . . G . | * . . . | . * . . | . . * . | . . . * .
-
Note how the entries on the left side of the table remain mostly consistent when compared with hexatonic marwa and hexatonic todi.
* Suspended pentatonic - 23232 - D-E--G-A--C-D - EADGC - pentatonics E=mangong;A=minor;D=suspended;G=ritusen;C=major * --5-7 D 55 - 25 - 52 32 - 37 D D -4--7 E 54 - 34 52 27 - 72 E E 3-5-7 G 43 55 - 25 23 - 37 - 73 G G --5-7 A 45 25 - 52 32 - 27 - 72 A A 3-5-- C 35 - 53 55 23 - 73 C C Unique: 35@C- 53@C 25@D - 25@G - 25@A 23&G - 23@C - 32@D - 32@A chord groups: . . . . . . . . . . . 435 = 435/543/354 = major . . . . . . . . 345 = 345/534/453 = minor 732 = 732/273/327 = minor 7 no 3 . . . 372 = 372/237/723 = minor 7 no 5 . . . . . 444 = 444/444/444 = augmented 741 = 741/174/417 = major 7 no 3 . . . 471 = 471/147/714 = major 7 no 5 . . . . . 525 = 525/552/255 = suspended 165 = 165/516/651 = flat 9 no 3 . . . . 156 = 156/615/561 = flat 9 flat 5 no 3 . . . . 363 = 363/336/633 = diminished 462 = 462/246/624 = dominant no 5 . . 426 = 426/642/264 = major flat 5| * . . . | . * . . | . . * . | . . . * . | D . E . | . D . E | C . D . | . C . D . | . . C . | A . . C | . A . . | G . A . . | . G . A | . . G . | E . . G | . E . . . | D . E . | . D . E | C . D . | . C . D . | . . C . | A . . C | . A . . | G . A . . | . G . A | . . G . | E . . G | . E . . . | * . . . | . * . . | . . * . | . . . * .
-
Hexatonic Todi is the backwards, of one of the inversions of hexatonic blues, and it sounds like the blues, it has an extra major triad whereas Marwa has an extra minor triad
* Gujari Todi - 123231 - Rd-e--g-a--cR - EADGC - pentatonics E=mangong;A=minor;D=suspended;G=ritusen;C=major * -4-6- r 54 r 36 74 51 - 56 24 r --5-7 D 55 - 25 - 52 37 - 32 D 41 61 D 34--7 E 54 - 43 - 34 52 72 - 27 E 63 E 3-567 G 43 25 - 55 73 - 23 - 37 G 33 15 - 16 46 G --5-7 A 35 - 45 25 - 52 72 - 32 - 27 A 17 62 A 3-5-- C 53 - 35 55 73 - 23 C 65 C Unique: 35@A - 35@C - 53@C 25@D - 25@A - 25@G 23@G - 23@C - 32@D - 32@A 63@E 74@r 65@C - 56@r 46@G | * . . . | . * . . | . . * . | . . . * . | r D . E | C r D . | . C r D | . . C r . | A . . C | . A . . | G . A . | . G . A . | . . G . | E . . G | . E . . | D . E . . | r D . E | C r D . | . C r D | . . C r . | A . . C | . A . . | G . A . | . G . A . | . . G . | E . . G | . E . . | D . E . . | * . . . | . * . . | . . * . | . . . * .
-
Double harmonic major is a big thing in Hindustani music, they call it Bhairab
* Bhairab / Byzantine - 1312131 - SR--GM-PD--NS * 57 S 34 - 35 25 S *All* 61 - 65 44 S 5 R 35 - 45 32 - 72 R 36 41 - 71 15 - 51 26 - 42 - 62 R 5 G 35 - 45 - 53 - 54 23 G 63 14 - 74 65 44 G 5 M 45 - 54 55 M 36 14 - 41 15 - 51 24 - 46 - 64 M 7 P 43 - 53 52 P 33 17 - 47 16 - 56 26 - 42 - 62 P 7 D 34 - 43 - 53 - 54 27 D 63 17 - 71 61 44 D 7 N 34 - 43 37 - 73 N 33 47 - 74 16 - 56 24 - 46 - 64 N Unique: 35@S - 35@R - 35@G - 53@G - 53@P - 53@D 25@S 23@G - 32@R 65@S - 65@G - 56@P - 56@N 46@M - 46@N - 64@M - 64@N 47@S - 47@P - 47@N - 74@S - 74@G - 74@N 44@S 63@G - 63@D | * . . . | . * . . | . . * . | . . . * . | S R . . | N S R . | . N S R | . . N S . | D . . N | P D . . | . P D . | M . P D . | G M . P | . G M . | . . G M | R . . G . | S R . . | N S R . | . N S R | . . N S . | D . . N | P D . . | . P D . | M . P D . | G M . P | . G M . | . . G M | R . . G . | * . . . | . * . . | . . * . | . . . * .
-
(There actually is no recognized Hexatonic Purabi but it sounds like the blues)
* Purabi - 132231 - Ra--c-d-e--gR - EADGC - pentatonics E=mangong;A=minor;D=suspended;G=ritusen;C=major * -4-6- r r 44 71 - 74 51 - 56 24 - 26 r --5-7 A 45 25 - 52 72 - 32 - 27 A 41 61 A 345-- C 35 - 53 55 23 - 73 C 44 14 64 C --567 D 55 - 25 - 52 37 - 32 D 15 - 16 46 - 42 D -4--7 E 54 - 34 52 72 - 27 E 44 17 62 E 3-5-7 G 43 55 - 25 23 - 37 - 73 G 47 65 G Unique: 35@C - 53@C 25@A - 25@D - 25@G 23@G - 23@C - 32@A - 32@D - 44@r 47@G - 74@r 65@G - 56@r 46@D - 64@C | * . . . | . * . . | . . * . | . . . * . | r A . . | G r A . | . G r A | . . G r . | E . . G | . E . . | D . E . | . D . E . | C . D . | . C . D | . . C . | A . . C . | r A . . | G r A . | . G r A | . . G r . | E . . G | . E . . | D . E . | . D . E . | C . D . | . C . D | . . C . | A . . C . | * . . . | . * . . | . . * . | . . . * .
-
* Classical modes - D-EF-G-A-BC-D - BEADGCF - B-locrian, E=phrygian, A=aeolian, D=dorian=2122212, G=mixolydian, C-ionian, F=lydian * 3-5-7 D 43 - 45 *All* *All* D 63 D -45-7 E 34 - 45 - 54 25 - 52 27 - 32 - 72 E 14 - 47 - 74 65 E 3-56- F 35 - 53 55 23 - 73 F 33 41 - 71 15 - 51 26 - 46 F 3-5-7 G 35 - 43 - 53 *All* 23 - 32 - 37 - 73 G 17 62 G -45-7 A 34 - 45 - 54 *All* 27 - 32 - 37 - 72 A 14 64 A -4-67 B 34 - 54 52 27 - 72 B 36 47 - 74 16 - 56 24 - 42 B 3-5-7 C 35 - 43 - 53 25 - 55 23 - 37 - 73 C 17 - 41 - 71 61 C Unique: 35@G - 35@C - 35@F - 53@G - 53@C - 53@F 63@D 23@D - 23@G - 23@C - 23@F - 32@E - 32@A - 32@D - 32@G 25@E - 25@A - 25@D - 25@G - 25@C 47@B - 47@E - 74@B - 74@E 65@E - 56@B 46@F - 64@A | * . . . | . * . . | . . * . | . . . * . | D . E F | . D . E | C . D . | B C . D . | . B C . | A . B C | . A . B | G . A . . | . G . A | F . G . | E F . G | . E F . . | D . E F | . D . E | C . D . | B C . D . | . B C . | A . B C | . A . B | G . A . . | . G . A | F . G . | E F . G | . E F . . | * . . . | . * . . | . . * . | . . . * .
-
Here are the 3 note closed position chords and inversions for M3 tuning. All possibilities. Some chords have alternate shapes but I won't list them as that can be learned at a later time. Will use 6 string guitar as the base. Its pretty much the same anyways
Augmented
Root - x111xx
1st Inv - xx111x
2nd Inv - xxx111
Major
Root - x221xx
1st Inv - xx212x
2nd Inv - xxx122
Minor
Root - x211xx
1st Inv - xx112x
2nd Inv - xxx121
Diminished
Root - x321xx
1st Inv - xx213x
2nd Inv - xxx132
Quartal
Root (Straight Fourths) - x123xx
1st Inv (Or Sus4 Root) - xx231x
2nd Inv (Or Sus 2 Root) - xxx312
7th (No 5th)
Root - x113xx
1st Inv - xx131x
2nd Inv - xxx311
7b5 (No 3rd)
Root - x133xx
1st Inv - xx331x
2nd Inv - xxx313
Major 7th (No 5th)
Root - x114xx
1st Inv - xx141x
2nd Inv - xxx411
Minor 7th (No 5th)
Root - x214xx
1st Inv - xx142x
2nd Inv - xxx421
7th (No 3rd)
Root - x143xx
1st Inv - xx431x
2nd Inv - xxx314
Maj 7th (No 3rd)
Root - x144xx
1st Inv - xx441x
2nd Inv - xxx414
Maj7b5 (No 3rd)
Root (Lydian) - x134xx
1st Inv (Or Locrian Sus4b5 Root) - xx341x
2nd Inv (Or Phrygian Susb2 Root) - xxx413
Maj7sus4 (No 5th)
Root (This one sounds Lydian to me strangely enough) - x124xx
1st Inv (Or Lydian Sus#4 Root) - xx241x
2nd Inv (Or Locrian Susb2b5 Root but honestly this one sounds like Lydian too) - xxx412
The ones I just listed are all in the 4 fret area with adjacent strings. Things would get harder from here as there are non-adjacent strings involved and wider Stretches. Wider Stretch Chords I recommend in higher frets.
7sus2
Root - 75x5xx
1st Inv - x5x53x
2nd Inv - xxx531
Min/Maj 7th (No 5th)
Root - 65x5xx
1st Inv - x5x52x
2nd Inv - xxx521
Maj7#5 (No 3rd)
Root - 5x54xx
1st Inv - xx541x
2nd Inv - xx85x5
Maj7sus2 (No 5th)
Root - 75x6xx
1st Inv (Or Dorian Root) - x5x63x
2nd Inv - xxx631
7susb2 (No 5th)
Root - 85x6xx
1st Inv - (Or Major Sounding Root) x5x64x
2nd Inv - xxx641
Cluster
Root - 85x7xx
1st Inv - x5x74x
2nd Inv - xxx741 (Yeah screw this one lol)
That's pretty much all the 3 note chord possibilities in closed position. Surprisingly there aren't that many! Good luck to the Major 3rd Tuners out there. May this list help you as a referenceLast edited by jazznylon; 02-11-2020 at 09:16 PM.
-
Thank you, blessings upon you. Good luck upon the work for these revelations. I understand your notation and I see that we have recognized the same set of triad groups going by the upper list which you provided. With the basic shapes the inversions are rapid and easy and the meaning of them leaps out, and the joy of that is something that you mainly get by using this tuning as compared to other tunings. But see where we are looking at it different is, I am looking at it upside down compared to you. For example on the major triad I can see by how you defined the named triad plus its inversions, as well as on the other triad groups. For major you have x221xx, that corresponds to the shape I identified as "543 aka 43". Whereas I had named "435 and it's inversions" as major, and, 435 in my notation is xx212x in your notation. We are upside down from each other. See you have the root note of the triad as the lowest note and I have it as the highest note. My reasoning is, because, the highest note in a triad is the one that has to correspond with the melody. The highest note of a triad is the one being colored, the lower two notes of a triad are the ones doing the coloring. For example. Mary had a little lamb. "Mary had a" is single notes. Lamb is a triad. Note note note note note note triad. Check it and you will see, I think, that whatever triad shape you use for Lamb, it only works if Lamb is the top note of the triad, you can try it with lamb as the middle note or lamb as the lower note, but it works real good with lamb as the highest note. So the location of the triad must be the location of lamb. So many riffs are like that, they go note note note note note and every once in a while they go triad. You're going note note note and suddenly there's a triad, but the triad is going to decorate a certain note, we are saying this note shall be decorated by two other notes and yet remain the dominant note. Really diads are even more versatile. You almost always color a note with the 5th - 5 semitones under the note - if it's there in the scale, and it would be 7 semitones if it were above, but 5 semitones below.
Additional Treasure on 01/07/2021, paste this into notepad for the columns to line up somewhat:
Note the layout, here is the hidden secret you have searched for, here is the unifying theme.
This is the circle of fifths, BEADGCF, from B to E is 5 semitones, E to A is 5 semitones, etc:
This is the secret hidden in plain sight, I do not expect acknowledgment and neither should anyone, it must be "wielded" not acknowledged:
.
in notepad replace all, .............. with ................................ for wider less imperfectly spaced chart
.
.
B.............E.............A.............D....... ......G.............C.............F.............
-.............-.............-.............-.............-.............-.............-.............
54/34.........54/34.........54/34.......................35/53.........35/53.........35/53.........
..............45............45............45/43.........43............43....................... ...
-.............-.............-.............-.............-.............-.............-.............
52............52............52/55.........52/55.........52/55.........55............55............
..............25............25............25...... ......25............25..........................
-.............-.............-.............-.............-.............-.............-.............
27............27............27/37.........27/37.........37............37....................... ...
..............32............32............32/23.........32/23.........23............23............
72............72............72............72/73.........73............73............73......... ...
-.............-.............-.............-.............-.............-.............-.............
74/47.........74/47................................................ ...41/71.........41/71.........
..............14............14.................... ......17............17..........................
-.............-.............-.............-.............-.............-.............-.............
B.............E.............A.............D....... ......G.............C.............F.............
-.............-.............-.............-.............-.............-.............-.............
56............65.................................. ....................51............61............
15................................................ ..................................16............
-.............-.............-.............-.............-.............-.............-.............
............................64.................... ..................................46............
42................................................ ......62........................................
24................................................ ..................................26............
-.............-.............-.............-.............-.............-.............-.............
36........................................63...... ..................................33............
-.............-.............-.............-.............-.............-.............-.............
4.............4.............4.............3....... ......3.............3.............3.............
7.............7/5...........7/5...........7/5...........7/5...........7/5...........5.............
-.............-.............-.............-.............-.............-.............-.............
B.............E.............A.............D....... ......G.............C.............F.............Last edited by KooksAmass; 01-07-2021 at 01:53 PM.
-
Indeed. I do not know which great composer said that the important thing, in a chord, is the bass and the upper note, and that all kinds of things can happen in between. Ted Greene has two ways to specify chords, by bass and melody. I often spot them like this myself, because it's easier to find them on the guitar in this way
 Originally Posted by KooksAmass
Originally Posted by KooksAmass
on the general discussion of this tuning, I find it interesting, but never used it, although I played 7 strings since the 80s (tuning A E...), and since last year the 8 strings. I tune it F# B E A D G B E, in fact a whole tone lower E A D G C F A D, which allows to find the chord forms of "normal" tuning of the 6 strings, and the same fingerings on the bass strings, with a tuning in fourths. If I learned the guitar now I would tune it entirely in fourths, but that would require re-learning all the ratings slots, scales and chords
I have no criticism to make to your tuning, I just have a question: how sound acoustically the guitar tuned in major thirds, because we have less natural harmonics?
-
In response to the other question, the quality of the sound is case by case. You are playing one note. Is that really the note? Is there something wrong with the string? Now two notes. Are both of the notes real notes? Is the fact that the un-fretted two strings would not be 5 semitones apart, a problem? Or is all that matters that you have two fretted notes and they are a certain interval apart? Who knows. Now three notes, etc. After the discussion is completed, I will put a link to one of my raga attempt videos up here, you can see the issues I am struggling with on this Indian classical music. My teacher never expected me to play any chords at all, Indian classical music doesn't have chords, but it does have a way for chords, and I think that for this and for heavy metal and any kind of jazz that is heavy on triads then it is a good system. My teacher lets me play chords, sometimes he might say use less chords for a minute. But my teacher enforces the raga stuff on me, and anything I do with the chords must integrate with that, and the choices overwhelm me due to my skill level and it interferes with my music. After a month on the same raga, I finally am having less trouble integrating the chords, and I still have to deal with the raga stuff. Anyone using this tuning, I really recommend you get a Sitar player for a teacher, they won't care about how you tune your instrument, and that will help you. My teacher after all these years still doesn't even know that my tuning is all exotic and weird, he has no idea, and we don't talk about theory ever but for a second. [[let me leave that grave stone in place for a minute] * [2/12] in response to the bitter whiner Patloch who expects me to care about his problems *, the tuning is terrible on a 6 string guitar, the range is reduced so it has to be 7 strings. The reduced range is so frustrating. Its magic with 7 strings. 7 strings almost goes without saying. 6 strings didnt even occur to me. You raise an interesting point though, and that is, if you must use 6 strings, I recommend you truncate at the low end of the range, if for example you would span from E to E with 7 strings then in the case of 6 strings lose the low E and keep the top E in other words, which may be contrary to ones intuition. With 7 strings I recommend your favorite root note to be the 2nd lowest string so that you can play it open in a unison diad with the same note on teh 1st lowest string. It's the mappings of the triads within the scales which is actually the point of all this and they only span 4 strings and then they repeat. If you really want to dig the point of this thing, stare at the Classical Mode chart for a little while, with understanding of my notation, and in particular, gaze at the left side of the Classical mode chart, I am pretty sure something interesting would leap out at you. Folks this is a lonely path and only success in the field will be a victory over guys like our colleague who will live in infamy as an example of who to pay no heed to on this march, therefore abandon complacency and seek for large goals through much practice. I do not respond to you on the thread because I would not want to update the timestamp on the thread and therefore continue the discussion and litter the archive of my treasure with your nonsense. Here is a recent youtube video I put up, as a record of my progress. In those videos you can hear me struggling with raga issues, more so than demonstrating the virtues of the tuning, but here I am beginning to get some strength. Theres stuff up there from years back which I did that was more beautiful, on just straight improvising. But on ragas you have to introduce certain notes of the scale in order, gradually increase the tempo, hit all these rhythm permutations, hit a bunch of gimmicks, most desperately of all improvise in harmony with a series of refrains, that is difficult, and there are special timing gimmicks without which the listeners brain would not track onto the rhythm. The mastery of it is in practicing the special weird complicated endings to solos, everything is mastered by adding another layer of complexity, only when you can do XY and Z can you truly even do X. Note that the triads are not just for chords but they are also map out all of the basic arpeggio patterns, you hear me on here using plenty of diverse stuff from the charts as arpeggios. December 29 2020 I changed the youtube video to one which I am more proud of. ]
Last edited by KooksAmass; 01-01-2021 at 12:21 PM.
-
actually, I didn't understand why this topic didn't start by simply and clearly presenting this system for 6-string guitar, unless it was done previously, or the 7-string switch brings something really new (I also plays the 7 and 8 strings)
Major thirds tuning wikipedia
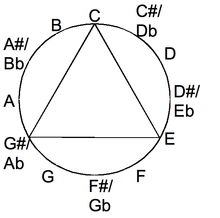 after all, it reminds us of the great steps of a certain John Coltrane...
after all, it reminds us of the great steps of a certain John Coltrane...
perhaps this would have avoided some mockery, which we do not know if they relate to the tuning itself, or its presentation, which actually confines to the cemetery of guitar elephants. If it took me a while to figure something out, it's because I prefer cremation to burial



 Reply With Quote
Reply With Quote







Part 2 Secrets to McCoy Tyner using 4ths,...
Today, 07:31 PM in Improvisation